yxCoding

I am a coder

KMP字符串匹配算法笔记

yxjoey posted @ 2008年3月25日 00:40 in C语言 with tags c 程序 KMP , 8960 阅读

 

网上有很多解释KMP算法的文章，A_B_C_ABC的这篇很详细，反复看了好几遍，总算理解了个大概，但是总觉得没那么爽快。其实，一种算法各人有各人的理解方法，找到适合自己理解的才容易记住。下面是我对这个算法的一些理解：


最普通的字符串匹配算法就不记了，简单贴一下代码

  1. int strstr(char *sub, char* str){
  2.         int i=0;
  3.         char *p=str, *q=sub;
  4.         while(*(p+i)!='\0'&&*(q+i)!='\0'){
  5.                 if(*(q+i)==*(p+i))
  6.                         i++;
  7.                 else{
  8.                         p++;
  9.                         i=0;
  10.                 }
  11.         }       
  12.         if(*(q+i)=='\0')
  13.                 return p-str;
  14.         return -1;
  15. }

 

下面说说我理解的KMP算法，与普通匹配算法不一样的是，KMP算法在子串匹配失效的时候，下一步并不是重新从子串的头部开始匹配，而是根据一下next函数计算出下一步应该从子串的什么部位开始匹配。举个例子更容易说明

红色为失效位置, '^'表示的当前是指针位置，'～'表示此次匹配A串开始的位置。

若是普通的匹配算法，当失效时，C串指针要回溯到头部，A串指针也要回溯到'~'的下一位。也就是下一步应该是从A的第二字符(e.g. 'b')和C的开头(e.g. 'a')开始匹配。如此循环

 

直到找到A串中的某一个位置可以匹配C串。

然而从上面的匹配过程中，可以发现A和B的蓝色部分是第一步中已经确认匹配过的，上面四步的匹配其实可以看作是蓝色部分的前半段与后半段在进行比较，而且前三步在蓝色部分就已经匹配失效了，所以这些比较是无谓的，因为它与父串A无关的，是属于子串C本身的信息。只有第四步才涉及了与父串A中的字符('c')的比较

KMP算法正是利用这一点，它事先利用子串本身的信息就计算出当某一次匹配失效时，下一次应该继续匹配的位置。也就是当C串在最后一个'b'匹配失效时，它省略了前三步(1,2,3)无谓的匹配，下一步比较将在'd'与'c'之间进行。这样父串A无需回溯，C串用一个next函数决定它将回溯的位置。所以next函数至关重要，也是这个算法的关键。

从上面的分析可以知道next函数是子串C本身的性质决定的

假设子串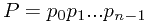$P = p_0p_1...p_{n-1}$

next(j)=k(k>=0): 当P的第 j+1个字符 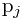p_j匹配失败时, 在父串指针不回溯的情况下，下一步将与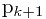p_{k+1}比较。next(j)的函数计算可以表达为

$$next(j)= \left \{ \begin{array}{ll} maximum(k), when\hspace{1mm}0\leq k <j\hspace{1mm} and\hspace{1mm} p_0p_1....p_k = p_{j-k}p_{j-k+1}....p_j & (1)\\ -1, otherwise & (2) \end{array} \right.$$

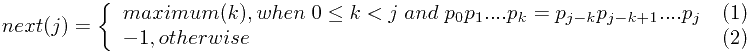
当next(j)=k (k>=0)时，子串指针回溯到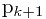p_{k+1}的位置，父串指针不变；
当next(j)=-1时，子串指针回溯到头，父串指针前进一步；

在设计计算next值的程序的时候，我们没有必要每一步都去计算maximum(k)，可以用递归方式来做

举个例子
假设子串为P:"abacabab", 且我们将要求的是'b'的next值, e.g. next[7]
假设next[0~6]均为已知: next[0]=-1, next[1]=-1 , next[2]=0 , next[3]=-1 , next[4]=0 , next[5]=1 ,next[6]=2

    "abacabab"

next[6]=2可以说明P[0~2](蓝)与P[4~6](红)是一样的

要求next[7]的值，我们可以找前6位("abacaba")中最长的前半段与后半段相等的子串，然后比较前半段子串的下一位是否和P[7]相等。在这个例子中, P[0~next[6]](e.g. P[0~2])就是这样的子串，接下来我们比较 c 和 b也就是P[next[6]+1]('c')和P[7]('b').

  • 若相等则 next[7] = next[6]+1
  • 若不等, 我们进一步找更短的前半段与后半段相等的子串,因为aba和aba是一样的, 要找'abacaba'中比'abc'短的这样的子串,相当于找'aba' 中的next[2]值是一样的.也就是next[next[6]]的值。然后再比较P[next[next[6]]+1]和P[7]是否等，若不等则继续找更短的这样子串


在上的例子中 P[next[6]+1]=P[3]('c') ，与P[7]('b')不相等， 但是  P[next[next[6]]+1] = P[next[2]+1] = P[1]('b'), 与P[7]('b')相等

最后可以得到next[7] = next[next[6]]+1 = next[2]+1= 1;

计算next值的代码：

  1. void calnext(char* P, int next[]){
  2.     next[0] = -1;           //第一个元素的next总是-1, 因为根据(1) , 我们并找不到一个k比j=0小
  3.     for(int i=1; i<strlen(P); i++){
  4.         int k = next[i-1];     //因为采用递归的方法, 为了计算next[i], 先记录下next[i-1] 而且假设next[i-1]已知
  5.         while(P[k+1]!=P[i]&&k>=0){ // 递归
  6.             k = next[k];
  7.         }
  8.         if(P[k+1]==P[i])     //如果相等而结束, 则找到一对长度为k的前缀字串和后缀字串
  9.             next[i] = k+1;       //增加了一个相同项
  10.         else
  11.             next[i] = -1;          //其他情况
  12.     }
  13. }

匹配的代码:

  1. int find(char*T, char* pat){
  2.     int n = strlen(pat);
  3.     int *next = new int[n];
  4.     calnet(pat, next);
  5.     char *p=T, *q=pat;
  6.     int i=0;
  7.     while(*p!='\0'&&(*(q+i)!='\0')){
  8.         if(*p==*(q+i)){
  9.             p++;
  10.             i++;
  11.         }else{
  12.             if(i==0)
  13.                 p++;
  14.             else
  15.                 i = next[i-1]+1;
  16.         }
  17.     }
  18.     if(*(q+i)=='\0')
  19.         return p-T-n;
  20.     else
  21.         return -1;
  22. }

记录一下自己理解的KMP以免以后自己都忘记当时怎么理解的。

Small_feed 评论 (0)

yxjoey

分类

标签云

最新评论

最新留言

友情链接

我的豆瓣收藏

浏览计数器

64203
designed by: Website Builder | coded by: Web Hosting Geeks | Host by is-Programmer.com | Power by Chito 1.3.3 beta