今天在网上闲看,发现最近正在举行2008年百度之星大赛,于是看看了历年试题,挺有意思的
2005年有一道题目是这样的
15=1+2+3+4+5
15=4+5+6
15=7+8
请编写程序,根据输入的任何一个正整数,找出符合这种要求的所有连续正整数序列。
输入数据:一个正整数,以命令行参数的形式提供给程序。
最近正好在找实习,肯定会遇到当场写代码的,于是写下这个程序算个练习
连接字符串A, B,但是要求把字符串A的尾部和B的头部重复的地方合并;
例如:
A: "12345"
B: "45678"
那么A+B = "12345678";
我第一个想法就是对A的每个位置都去检测剩下的是否和B可以合并,不过实现的效率很低O(strlen(A)*strlen(B)). 程序如下:
题目是这样的:写程序判断是否字符串A里每个字符在A中出现的次数都大于在字符串B中出现的次数。
我的想法是
1. 首先我们可以发现,如果判断成立的话,A的长度必定要比B的长度长。
2. 因为字符char的大小有限,所以可以建立一个对应所有字符的数组,一般情况下应该是char chars[2^8], 初始化为0,然后先统计A串中所有出现的字符的个数。对于A的字符c,我们可以用chars[c]++来进行统计。在统计完毕之后,对于B的每个字符进行反向统计,即对于B中的字符c', 计算chars[c']--。若在对B的统计过程中,有某一chars[c']<=0,这说明对于字符c',它在B中出现的次数不比A中少,由此返回0, 若所有chars[c']均满足chars[c']>0,则返回1。
号称是Google的面试题:输入a_1, a_2, ..., a_n, b_1, b_2, ..., b_n,如何在O(n)的时间,用O(1)的空间,将这个序列顺序改为a_1, b_1, ..., a_n, b_n。
初看此题,觉得挺好理解。如果不满足时空复杂度,这道题非常简单。这道题的关键就在于如何优化时空复杂度。
对于每个元素的最终位
置可以用如下这个公式来计算.
-
//For an element a[i], its new place will be i>=n/2?(i-n/2)*2+1:2*i
-
int new_pos ( int i, int n ) {
-
%nbsp return i>=n/ 2 ? ( i-n/ 2 ) * 2 +1 : 2 *i;
-
}
题目是这样的:题目大概是这样的,一个金字塔,它的每个位置都有一个数字(如下图所示),顶端有一个小球,小球下落时经过任何位置都是等概率的。现在要求的是小球从顶端下落到低端的路径中,数字和最大的路径
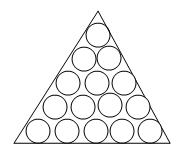
我的解法是用%ldquo动态规划法%rdquo,用一个二维数组pyrimid表示当前的金字塔,在小球的下落过程中,对于每个位置pyrimid[i]][j],它的前一个位置只有两个选择pyrimid[i-1][j-1]或者pyrimid[i-1][j],因此我的算法就是依次计算每个位置的累计数字值,然后在最后一层选取最大的。下落路径可以一步一步反推回去,它的程序如下:
一个整数数组array, 在所有的子数组(从下标i到下标j)中最大的和,要求时间复杂度为O(n).
举个例子 int array[]={1, 4, -5, 9, -2, -5, 4, 1}, 最大的子数组和为9(从0~3或者4~4)
简单来说
深度优先搜索用递归实现
- 输出当前结点
- 对于当前结点的所有子结点,依次递归运用深度优先搜索
广度优先搜索用队列实现
- 将起始结点入队列
- 循环(队列非空)
- 取出一个结点
- 输出结点内容
- 将此结点的所有子结点入队列
将有序的两个链表合并成一个有序链表。 下面的程序分别实现了修改原链表和不修改原链表的方法
今天复习的时候遇到这个题目,觉得挺有意思,而且搜索一下,网上解法各式各样,从冒泡,选择..到快速排序,堆排序。我不是想得到效率最高的算法,只是想练习一下。
yxjoey
